村上雅人が海鳴社から出版している、おもに教養学部の大学生を対象とした数学のシリーズです。高校生でも、ある程度分かる内容になっています。数学シリーズを執筆するきっかけを「バウンダリー」という月刊誌に書いて欲しいと、同誌を発行しているコンパス社の小林文武編集長に依頼されて、まとめた文章を一部修正して掲載しました。近日中に、シリーズの正誤表も本ウェブに掲載する予定です。
私が数学書を書いたわけ
芝浦工業大学 村上雅人
1. はじめに
最近、海鳴社という出版社から、続けて数学書を出版している。数学シリーズの既刊は「なるほど虚数」「なるほど微積分」「なるほど線形代数」「なるほどフーリエ解析」「なるほど複素関数」「なるほど統計学」「なるほど確率論」の7冊である。この後、ベクトル解析、回帰分析、微分方程式、偏微分方程式、特殊関数などの数学分野を網羅することを考えている。
そして、数学が片づいたら、引き続き、電磁気学、熱力学、量子力学などの理工系分野にも手を広げることを考えている。ただし、構想があまりにも壮大なので、自分でもいつまで続くのかは見当がつかない。しかし、ライフワークのひとつと考えている。
将来的には、熱力学や量子力学で疑問になっている点を明らかにして、自分なりの学問領域を構築したいと思っているが、本業があるので、夏休みや土日の開いた時間しか使えない。よって、どこまで進めるかは本人にも分からない。しかも、最近では土日が研究論文などをまとめる日になっているので、執筆の時間はどんどん減っている。
電子機器が発達しているので、電車に乗っている時間を執筆に当てるもこともできるが、これは危険である。なぜなら、ついつい自分の世界に没頭してしまい、降りる駅を通り過ぎてしまうからだ。つい先日も、自宅のある荻窪駅で降りるはずだったのが、気づいたら国分寺駅であった1。
2. きっかけ
もともと小学校のころから数学が好きであった。これは、ものぐさな性格に由来している。なぜなら、数学は基礎さえしっかり押えていれば、あまり勉強しなくもと合格点が取れるからである。他の科目では、多くのことを暗記しなければ落第してしまう。
しかし、動機はどうあれ、いつのまにか数学が本当に好きになった。その理由は、数学には例外がないので、首尾一貫した論理展開ができる点にある。他の科目は例外だらけであるので、個人で勉強するのは難しい。
高校時代にアメリカへ留学した経験も大きな影響を与えている。最初のころは言葉がなかなか通じなかったが、数学をする限りは言葉の問題はなかった。みんなができない数学の問題を解いてみせると、ヒーローになった。
当時、カリフォルニア州の数学コンテストで2位になったことも自信につながっている。日本では、高校生の平均的な数学レベルはアメリカよりもはるかに高い。しかし、アメリカでは本人がその気にさえなれば、高校生であっても、いくらでも高いレベルを目指せるのである。しかも、大学入学においては、その点も考慮される。そんなわけで、カリフォルニア州でも、全州にわたった数学コンテストが開かれていて、各高校から数学自慢が集まって腕試しをするのである。ただし、日本の大学入試問題の方が難問ぞろいという印象を受けた。今でも、いくつかの設問を覚えている。例として、わたしが間違えた問題を紹介すると、それは
問 行きを時速50マイル、帰りを時速60マイルで走ったときの平均時速を求めよ。
という問題であった。距離が明示されていないので、どうやって解いたら分からないとコンテストに参加した多くのアメリカの友人は言っていた。よく考えずに
とやって、時速55マイルが平均時速と答えたものも多かったのである。
この問題は、片道の距離をDマイルと仮定する。すると、行きにかかった時間は
であり、帰りにかかった時間は
となる。よって、往復に要した合計の時間tは
と与えられる。往復の平均時速は、その距離2Dを、走行に要した時間tで割ればよいので
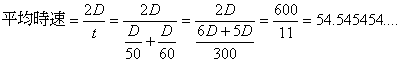
となる。さて、ここで問題が生じた。答えをどう書くかである。当時の日本の入試問題対策マニュアルによれば、問題に出されている数値と同じ有効数字にしろという指示が書いてあった。すると、この場合は小数点以下は有効ではないので、四捨五入すると55となって、何も考えずに50と60の平均を求めた場合と同じになってしまう。
いろいろ悩んだすえに、裏の裏のまたその裏をかいて、時速55マイルと書いたのであるが、正解は54.5あるいは54.54…であった。
こんな問題に引っかかった自分が情けないと悔やんだが、普通に考えれば、かっこして54.5454..と併記していれば、（アメリカでは）正解にしてくれたに違いない2。この他にも、ポーカーでスリーカードが出る確率や、多元連立1次方程式の解を逆行列を使って求める問題や、スターリング近似式を導出する問題など、多岐に亘っていた。
ちなみに、全問正解で1位になったのは、中国人3世の女子高生で、いまは州立大学の数学科の教授をしている（らしい）。上位をアジア系が独占したことで、地方新聞にアジアンパワーと紹介された。
アメリカでは、希望さえすれば、高校生が大学の授業を自由に受けられる。実際に、いろいろな高校から授業を受けに来ていた。コンテストで1位になった彼女もほかの高校ではあったが、私と同じ大学で同じ講義を受けていた。数学担当の先生から、同じクラスから数学コンテストの1位と2位が出て名誉だと、みんなの前で誉められたことを今でも覚えている3。
3. 日本の大学の講義
その後、帰国して日本の大学に入学した。そこで驚いた。大学は、もっと自由なところかと思っていたが、あまり予備校と変わらない。しかも、議論などする時間などなく、講義は一方通行である。しかも、内容が分からない。不勉強のせいもあるのであろうが、講義で何を語ろうとしているのか、意味不明なのである。アメリカの大学の講義は、明快である。何をすればよいかがはっきりしている。しかし、日本の大学の講義では、何をすればよいかという指示の内容さえ不鮮明なのである。
中でも驚いたのは英語と数学であった。英語の教材は、日本語に訳しても意味が分からないようなもので、これが何の役に立つのであろうかと首を傾げたことを覚えている。最近、「理系のためのサバイバル英語」をはじめとして、理工系人間を対象にした英語の本が出版されているが、まさに自己防衛を理系の人間がはじめたということであろう。何しろ、ある外国のジャーナルには、日本人だけのために英語を矯正する旨の注意書きが書かれている。教養で純文学者のわけの分からない（古典）英語を読まされたのでは、論理性が重要視される理系英語など身につくはずもない。
数学にも困った。当時、理系の基礎は「線形代数」「微積分」「ベクトル解析」ぐらいであろうと思っていたが、教わる内容がアメリカと大きくかけはなれている。黒板に書かれている字も見にくく、記号も分からない。（今にして思えば?や?であったと思う）。まわりの同級生は、それでもせっせと黒板を写している。これならば、授業などせずに、プリントしたものを配ればよいのにと思ってしまうが、そんなことを言えば、危険分子とみなされかねない。
しかし、このままではいけないと思い、先生方が書いた教科書を大枚をはたいて買ったが、その内容がまた意味不明であった。いろいろと調べていくうちに、面白いことが分かってきた。「日本では、高校時代までは、比較的数学が好きだった生徒や、得意であった生徒が、大学に入ると、数学本来の厳密さについていけずに落ちこぼれる」のだそうだ。「本来、数学というのは精緻な学問であり、大学に入って早々に、それを身をもって覚えこませることが重要である。」と書いてある本もある。別の書物には「高校と大学の数学には、大きなギャップがあって、それを乗り越えなければ真の数学は身につかない。」とも書いてある。
しかし、アメリカで、こんな問題が指摘されているという記憶がない。高校生でも大学の授業を受けることができるし、その内容を理解することもできる。高校数学と大学数学の間にギャップがあるとも思えない4。
確かに、フェルマーの定理の証明をみても分かるように、数学には厳密さが必要であり、すこしの綻びがあっても瓦解してしまう。ワイルズの証明も、いったんは綻びが見いだされ、10年の努力が水泡に帰す危機に見舞われた。それは、数学の論理には一貫性が要求されるためである。だからと言って、初心者に過度の要求を与えるのはどうであろうか。ワイルズが数学に興味を持ったのは、単純にフェルマーの定理を証明したいという子供のころの夢があったからであって、最初から数学の厳密性に興味があったわけではない。
すべての学問について言えることであるが、何よりも大局的な視野にたって、その分野を眺めるという作業が重要である。最初から重箱の隅をつつくまねばかりしていたのでは、数学の面白さが失せてしまうであろう。といっても、一介の大学生が偉そうな話をしても、いくばくの影響を与えるものではない。敢えて言えば、数学嫌いの人数がひとり増えただけのことである。
4. 出版事情
その後、理工系のはしくれとして、専門課程に進んだ。選んだのは、金属工学であった。数学が嫌いなので、数学のいらない分野に進んだという同級生が多かったのを記憶している。
確かに、数学を駆使して研究をするということはなかったが、そうかと言って数学が無駄というわけではない。むしろ、理工系のすべてについて言えることであるが、研究をするには論理的なステップを踏む必要があり、それは、まさに数学と同じ手法である。ただし、数式ばかりに頼っていると、本質を見失うこともある。数学を乱用しない課程に進んだおかげで、数学に振り回されずに済んだと思っている。単純な数式では、説明できないものが多いということを体験として学んだ。
ただし、数学をうまく使いこなせれば、これほど強力な武器はないというのも事実である。しかし、日本だけのくだらない事情のために、数学好きや、高いポテンシャルを持った学生のやる気を失わせるのは、あまりにも投資の無駄であろう。
そこで、他の本に頼らなくとも、誰もが理解できる大学生用の数学テキストを書いてみようと思うようになった。そこで、あらためて大学数学の参考書を見てみると、まず感じたのは、薄いテキストが多いということである。これは、厚い本は読者にも出版社にも敬遠されるためだという。そう言えば、最近は本の厚みも内容も薄い新書が増えている。ある人は、この現象を皮肉って「週刊新書」と呼んでいる。確かに、翌週には異なるタイトルの新書が書棚に並んでいる。
これに関して面白い話を出版社のひとから聞いた。それは、内容がいい本が売れるわけではないという話である。本を買う人間は、本を全部呼んでから買うわけではないので、中身よりも装丁や見てくれが大事だというのである。
しかし、薄いからといって、数学の場合、その項数を削るわけにもいかない。当然の結果として、ひとつひとつの項目が短くなり、定理や公式などの導出過程を大幅に省くことになる。こうなると、読んでも訳が分からないので、ますます本が売れなくなる。まさに悪循環である。
苦肉の策で、出版社は教科書を先生に書くことを薦める。こうすれば、少なくとも生徒の数だけ毎年本が売れるからだ。ところが、教科書に指定しても、本を買わない生徒が増え続けているという。そこで、先生は本を買ったかどうかをチェックして点数をつけることまでするという。そのせいか、ある私立大学の先生が生徒に訴えられたという話を聞いた。学長あてに「○×先生は、生徒に自分のくだらない教科書を強制的に買わせている」という苦情が寄せられたのである。世も末という気がする。
さらに、教科書持込み可という試験まで登場したらしい。持ちこみ可ならば、買ってみようという生徒も増える道理である。ところが、驚いたことに試験が終わると、教科書をそのまま机の上に放り投げていく生徒が相当数いるという。本好きの私にとっては、にわかには信じられないことである。
そこで、出版社の友人に、私の構想を話してみた。すると、けんもほろろに、それは無理だろうと言われた。大学の先生から、このような本を出してみないかと持ちかけられることが山のようにあるが、売れたためしがないという。まして、数学の本ならば教科書にしない限りは無理だという。どの出版社に持って行っても同じ答えしか返ってこないよとも忠告された。少し冷静になって考えれば、確かにその通りであろう。
5. なるほど虚数
3年前の夏に、1週間ほどの休みをとることができた。最近では、ウィークデーは本来の研究活動よりも、雑用に忙殺されることが多く、休みは共著論文のチェックや自分の原稿執筆にあてるのが常である。ところが、その時は、たまたまProceedings用の論文整理がすべて終わり、久しぶりに自由時間がとれたのである。
そこで、ふと数学のことを思い出した。私が現在専門としている超電導の分野では、虚数を使うことが多い。例えば、交流帯磁率の遅れ成分を虚数を使って表示する。量子力学でも虚数が大活躍する。
修士論文をまとめている学生も、普段は虚数を使ってデータ整理をしている。そこで、何気なく虚数を使う意味を尋ねたところ、よく分からないと言うのだ。大学院で「超伝導」に関する講義を行っていたので、聴講している院生にも同じ質問をしたところ、彼等も虚数を使う意味が分からないという。
実は、虚数については、超伝導の専門家とのワイン談義でも、その意味について話題になったことがある。その時「虚数は実態を持ったものではなく、交流などのように物理量が変化するときに、その遅れ成分を記述する便利な数学的道具なのだ」という主旨の説明をしたことを覚えている。
実は、虚数が最初に導入されたのは、すべての2次方程式（quadric equation）
の解を求めるためであった。ご存知のように、この解は
で与えられる。ところが√の中（これを判別式と呼んでいる）が負となると実数だけでは解がないことになる。そこで
あるいは
という数を導入すると、すべての2次方程式に（重根を2個と数えれば）、2個の解が存在することになる。さらに、すべてのn次方程式にn個の解が存在することも証明できる。
しかし、これだけであれば、虚数の存在意義はそれほど大きくはなかった。実際に、虚数を封印していた数学の一派もあったのである。それが、飛躍を遂げるのは、その幾何学的側面が登場してからである。図1のように複素平面というものを考える。x軸が実数軸、y軸が虚数軸とした平面である。この平面を使うとすべての、複素数を表示することができる。ただし、それよりも重要な事実は、iが複素平面において90°だけ回転する回転演算子の働きをするということである。例えば、1からスタートしてiを掛けるという操作を行うと
のように、4回の作用で、もとに戻ってくる。この事実だけで、虚数の応用範囲は飛躍的に拡大したが、それが物理、特に量子力学の建設に重要な役割を果たすのは、つぎのオイラーの公式が発見されてからである。
これは高校でも習う公式であるが、数学史上最大の発見と言っても過言ではない5。先ほどの複素平面で表示すると、
というグラフは、図2に示すように、半径が1の円に対応する。よって単位円(unit
circle) と呼ばれている。つまり、この絶対値は1である。ところが、これを実数軸と虚数軸から眺めてみると、図3のようにsin波とcos波を与えるのである。結局
を作用させると、絶対値は不変のままで、縦方向にも横方向にも進む波の性質を付与することができるのである。量子力学において、粒子の波動性がよく話題になるが、数学的には何とを掛けるだけで波動性を付与することができる。
ここで、オイラーの公式に
を代入してみよう。すると
となるので、
という等式が得られる。よく見ると、たったひとつの等式に、数学で重要な指数関数（e）、円周率（?）、1、0そして虚数（i）がすべて含まれている。この式を数学の中で最も美しい式と形容するひともいるが、この素晴らしさを大学の教養課程の学生にぜひ実感してもらいたい。さらに、オイラーの公式を利用すると
を計算することもできる。頭の体操として、どんな値が得られるか少し考えて欲しい。（解答は文末）
そして、オイラーの公式をはじめとして、電気工学や物理分野で使われる虚数にどういう意味と効用があるかをまとめた本を執筆しようと思い立ったのである。
一度、書き出すと、あれも書きたい、これも書きたいと多くのことが頭に浮かんできたが、何とか1週間で、ほぼ1冊の本にまとめることができた。虚数の効用にまとを絞った本である。しかし、出版社に勤めている友人の助言もあって、実際に出版しようなどとは夢にも思わなかった。
その後、学生や友人に原稿を見せたところ、これは非常に分かりやすいので、ぜひ本として出版すべきと言われた。このとき、たまたま目についたのがバウンダリー誌に広告を出している海鳴社という出版社である。確か、「川勝先生の物理授業」という全3巻の本の広告が載っていた。実は、海鳴社からは「オイラーの贈り物」という数学書が出版され、この分野では珍しいベストセラーになっていて、私もその本を持っていたのである。そこで、だめもとで海鳴社に連絡をとってみた。
すると、編集者の辻信行6という方から連絡があり、「数学の企画はまず当たらない。教科書に使ってもらえるならば別であるが。」というコメントがあった。9割以上だめという覚悟があるならば、宅配便で原稿を送って欲しいということであったので、とりあえず体裁を整えて送ってみた。
翌日に、辻さんから「これから伺いたい。」という連絡が入った。体よく断られるのであろうと思っていたら、少し興奮ぎみで、「この内容ならきっと売れます。」という思いがけない言葉をいただいた。それから、とんとん拍子に事が進み、2ケ月も経たないうちに出版の運びとなった。原稿を読んだ辻さんが「なるほど」と思ったことから「なるほど虚数」と題名をつけることにもなった。
その後、数ヶ月で初版2000部が売れ、第2刷を発行することになった。辻さんから、読者から数学の「なるほどシリーズ」を出版して欲しいという要望があり、辻さんも同感なので検討して欲しいという依頼を受けた。そこで、前に書いていた原稿などに加筆して、「なるほど微積分」「なるほど線形代数」「なるほどフーリエ解析」「なるほど複素関数」を続けて出版した。
売れることが、どのようなことかという実感はないが、確かにいろいろな方面から反響があった7。当初の意図は、数学に意欲のある学生が、日本式の大学数学教育のせいで意欲を失わないようにというものであったが、むしろ一度数学に挫折した30代から40代のひとたちから、「なるほどシリーズ」を読んで、もう一度数学をやりたくなったという手紙をいただいた。著者としてこれほど嬉しいことはない。（学生にも読んで欲しいのであるが、本屋にさえ行かない学生が増えている現状では、無理な話かもしれない。）
6. 終わりに
数学者でもない人間、それも数学とは縁もなさそうな学科を出た人間が数学書をまとめるということは荒唐無稽に聞こえるかもしれない。しかし、専門家ではないだけに、より客観的に情勢を眺めることもできるし、何より、数学が理工系の研究の場で、どのように役立つかということを書くこともできる。
数学を専攻した友人に、「なるほど虚数」を見せたら、「確かに面白いが、数学者は数学が何の役に立つかにはもともと興味はないからね。」と言われた。これで納得した。それで数学者が書いた数学の教科書は味も素っ気もないのだと。しかし、数学の歴史的な発展をみると、確かに純粋数学としての発展史もあるが、新しい数学の手法が大きな影響を他分野に与え、それが、さらに数学の世界にフィードバックされて進歩してきたという歴史もある。何よりも、こんな便利な道具を、使わずに放っておくのは勿体ない。
このようなわけで、「なるほど数学シリーズ」は、今後も延々と続く予定である。一応本人の心積もりでは、数学のあとは物理に移って、「なるほど量子力学」をシリーズの最後にしたいのであるが、海鳴社が赤字覚悟であれば、「なるほど超伝導理論」という厚手の本を最後の最後に書くつもりでいる。
補遺 の計算方法
解） まず
と置いて、両辺の自然対数をとる。すると
となる。ところで、オイラーの公式において
と置くと
であるから、両辺の自然対数をとれば
これを先ほどの式に代入すると
結局
となって、実数となるのである。不思議としか言いようがない。これをもじって、「愛の愛情は2割そこそこ」という人もある。何事も「過ぎたるは猶及ばざるが如し」ということか。最後に、数学問題ではなくクイズ問題として、アメリカで好まれるものに
という等式がある。お分かりであろうか。ヒントは複素平面における虚数の働きである。（解答は後ほど掲載予定）
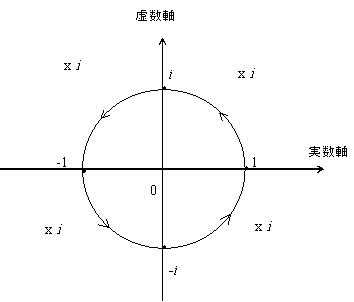
図1 1にiをかけるとiに、さらにiをかけると-1となる。このように、iをかけるという操作は、複素平面では90°の回転に相当する。
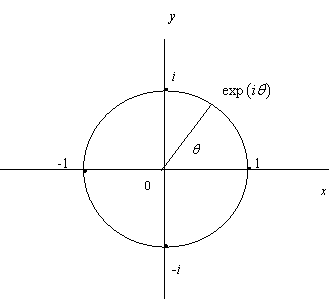
図2
は複素平面において半径1の円を描く。ここで、qの値が実数軸からの角度を与える。
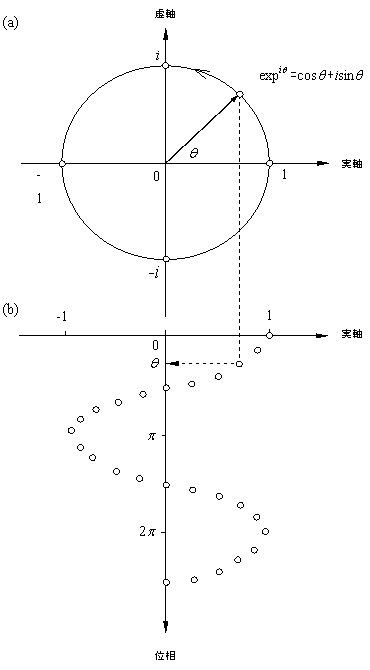
図3 複素平面における単位円上の回転（exp(i?)）は実数軸にはcos波を虚数軸にはsin波を発生させる。つまり偏角(?) を横軸にとると、実数軸の運動はcos??の波となる。
1 これには酒に酔って寝ていただけという指摘もあるが。
2 ただし、この問題は時速を40マイルと50マイルとしていれば、有効数字2桁であっても44マイルが正解になるので、出題としては、こちらを推奨したい。
3 あまり、先生に誉められたことがないので、記憶に鮮明に残っているのであろう。
4 アメリカの大学の教養では、日本の高校程度の数学しか教えないという指摘もある。しかし、ちゃんと大学レベルの線形代数を習った記憶がある。
5 大学の教養では、半年あるいは1年をかけて、この公式の意味と由来を考えることを推奨したい。
6 後に、海鳴社の経営者であることが分かった。だからこそ、出版を即決できたのであろう。
7 ここで売れるというレベルは2000部程度という意味である。